A Primer on Oblivious RAM
Efficient Obfuscation of Memory Access Patterns
We discuss the motivations and principles underpinning Oblivious RAM (ORAM) and the naive construction of one. We then transition to a more in-depth review of the drawbacks of older ORAM constructions, and how modern implementations like Path ORAM and Ring ORAM address them. Finally, we close on applications of these more efficient implementations, and their relevance to modern research in computer science and cryptography.
Note: This was a paper I wrote for Cryptography (ECE407) over the span of about 3 days straight. The literary quality dips in places and it's not my greatest work, but the topic overall is quite interesting. Hopefully you learn something new!
Table of Contents
Revisions
- 05/22: Client-side space overhead for Square Root ORAM was incorrectly characterized as \(O(N\log N)\)
Introduction
Oblivious computation research dates back as far as 1979. Pippenger et al. [1] explored the idea of an "oblivious Turing Machine", in which the motion of a Turing Machine's head on its tape lent no information about the underlying program. That is to say, you could make no useful conclusions regarding the input program by observing the head position - its movement was indistinguishable for any two input programs of similar length. This paper not only laid out the foundations for a functional OTM, but it also was the first paper to discuss the notion of oblivious computing. Computation in which the observable accesses and movements of a machine lent no information about the underlying operations.
In their seminal 1987 papers (later reunited as a journal paper in [2]), Goldreich and Ostrovsky extended the idea of oblivious computing to an off-CPU RAM that stored some sort of software. However, their motivation had more to do with software piracy. Since programs on a RAM were still just a sequence of bits, they could easily be copied and distributed by an adversary.
The knee-jerk solution to this problem would likely be to simply encrypt the data going in and out of the RAM. However, it's important to note that where and how memory is accessed can lend important information about the underlying program, especially when paired with a high-level description of what the program does (which you get by buying the software). For example - repeated reads of a cluster of adjacent RAM blocks could indicate some sort of loop structure within the program itself. This is obviously subject to some architectural decisions on the CPU's memory subsystem, but the point should stand as a motivating example. Thus, a system allowing for oblivious memory access should be able to mask not only what the data is, but where the data is and how the data was accessed.
Today's compute landscape presents other scenarios requiring security when accessing a RAM, outside of the initial goal of piracy-prevention. A large motivating factor, as outlined in [3] by Stefanov et al., is the advent of cloud compute. Many clients store secure data (tax forms, legal documents, etc.) on remote servers that are considered "untrusted". We also heavily rely on cloud compute for many modern services, many of which will inevitably require some amount of confidential information from the user.
In a naive security model where the client and cloud use symmetric encryption to prevent data from being leaked to eavesdroppers, the access pattern can still lend information regarding the type of actions that the client is engaging in with remote storage. Furthermore, the server has knowledge of the physical memory locations that the client accesses, which inherently lends insights into the off-server actions of the client. Thus, in the early 2010s there was a renewed interest in devising secure memory schemes enabling oblivious compute with untrusted remote servers.
[2] was seminal for many reasons. Today, we recognize it as the paper that defined the security model of Oblivious RAM, and outlined the basic schemes of implementing it that motivated future ORAM schemes for nearly 2 decades.
Problem Definition
The ORAM problem was first presented as two separate definitions in [2], found in sections 2.3.1 and 2.3.2. These refer to the definition of an ORAM to guarantee access pattern indistinguishability, then outline the definition of an ORAM "simulating" RAM as a way to prove correctness of the ORAM scheme. The aforementioned definitions are relatively obfuscated for the purposes of this primer (entrenched in Turing Machine models and whatnot), but there are some important takeaways to note.
- An ORAM system consists of a traditional RAM block and an ORAM protocol being run on the attached CPU. The RAM itself doesn't do any of the "obliviation", so to speak. This makes ORAM a bit of a misnomer, as it describes the perceived function of the RAM, not necessarily the function of the RAM itself.
- In any ORAM system, the client or CPU is considered secure. Memories inside of the client (registers, caches) and internal operations of the client cannot be determined by an adversary – they can only see the traffic between the client and the memory, and the data stored directly inside of the memory.
- To avoid leaking information through deterministic encryption or decision-making over multiple runs of the same program, any CPU involved in a feasible ORAM system must include some sort of random function and be able to make decisions based on it. In practice, this can be implemented as a PRF or PRG, with a randomly generated key or nonce used to vary the encryption of identical plaintext over different iterations.
Modern papers like [3], [4] prefer a simpler definition of the ORAM problem, and this is the one that we use going forwards.
Consider a sequence of memory accesses \(\vec{y}\), defined below, where \(| \vec{y} | = M\).
\[ \vec{y} = ((op_M, addr_M, data_M), ..., (op_1, addr_1, data_1)) \]
\(op_i\) denotes whether the i-th access is a read or write, \(addr_i\) denotes the address of the i-th memory access, and \(data_i\) is the data written into the RAM for a write access.
Given an ORAM algorithm, a sequence of logical client-server or CPU-RAM accesses \(\vec{y}\) is transformed into an observed access sequence \(\mathsf{ORAM}(\vec{y})\). ORAM protocols will guarantee that for any two access sequences \(\vec{y}, \vec{z}\) where \(|\vec{y}| = |\vec{z}|\), \(\mathsf{ORAM}(\vec{y}) \stackrel{c}{\approx} \mathsf{ORAM}(\vec{z})\). Furthermore, the data returned by \(\mathsf{ORAM}(\vec{y})\) must, with overwhelming probability, be consistent with the data returned by \(\vec{y}\) without the presence of ORAM (e.g "correct").
Throughout the rest of this primer, we refer to data in units of a single memory access, which we call a block. We also, for brevity, embrace a "client-memory" terminology to encompass all possible systems that may implement an ORAM scheme. While it is possible to have multiple clients share data access while employing an ORAM scheme (see Applications), a single-client model is adopted in this primer to simplify discussion of encryption and client-side state.
Implied Constraints of an ORAM
Given our earlier definition, we can start to determine some of the properties of what an ORAM should look like. The following section skims some of the high-level analyses in [2], and some personal understandings from reading various papers in the field. For starters, we can separate adversaries into two types.
- Non-Tampering Adversaries: Eavesdrops on the transactions happening between the client and the memory.
- Tampering Adversaries: Can actively write bad data into the ORAM, and do everything that a non-tampering adversary might.
Combating the additional actions of the Tampering adversary can be done via some sort of digital signature generated by the client that is stored with the data block. Reading a block with a bad signature could trigger some sort of error correction protocol. As a result, as alluded to earlier, the eavesdropping problem becomes the more difficult one to solve efficiently.
The indistinguishability criterion set forth earlier necessitates homogeneity of memory access pattern regardless of whether it is a read or write. Inherently, this means that every memory access will always have to read something out of the ORAM. Block writes would need to be batched and deferred to some later event, or you would need to always write back blocks (even on read operations). At a high level, regardless of the access type made, the actions being taken by the client should look identical.
There is also the problem of masking repeated accesses to the same data block – if the blocks are naively read/written to the same location between accesses, then it becomes easy to detect data reuse. As a result, any practical ORAM protocol will need to relocate or shuffle data blocks over execution.
Finally, since an ORAM breaks the implicit mapping of a block address or tag being used as a RAM index, we must attach additional metadata to each block in the ORAM to identify it after decryption. This metadata can include the block tag (encrypted with the block to avoid leaking mappings), a nonce used to randomize the encryption function, and any other properties that the ORAM protocol in question requires for correctness. It is generally assumed that any metadata required or suggested by a protocol is a fixed constant negligible to the size of the data block.
Inherently, each of the above properties requires access redundancy or additional computation over a naive RAM. The goal of the ORAM implementations presented in this primer is to maintain them while maintaining computational feasibility and ensuring a negligible failure probability.
An Early ORAM Construction
With the above objectives, one can think of some basic implementations of ORAM. An especially trivial one would be "brute force" – regardless of the memory access, you can read every block in the memory into CPU registers, optionally modify it, re-encrypt it with a new nonce, then write it back into the same location of the RAM. If a block needs to be reused later, it can be kept in the CPU for operation even after linear scan.
This scheme isn't all bad. For one, it doesn't require any special state about block mappings on the CPU – every block is exactly where you'd expect it to be, it's just that the server doesn't know which one you actually meant to use. However, the linear scan requires \(O(N)\) memory accesses given an N-block memory, and requires \(O(N)\) bandwidth. Any practical system would rattle to a halt. This motivated early research into devising an ORAM algorithm that was bandwidth-efficient (and, as a corollary, memory-access-efficient).
As if it weren't enough to design a security definition and objective for Oblivious RAM, Goldreich and Ostrovsky outlined early optimized ORAM schemes in [2]. We discuss their initial proposal of a Square Root ORAM and its pitfalls.
Square Root ORAM
This construction simulates an N-block RAM by using \(N + 2\sqrt{N}\) real memory blocks – an overhead of \(O(\sqrt{N})\) extra memory capacity (and the source of its name). Instead of brute-forcing the entire memory to hide its accesses, it permuted the order of its blocks and periodically reshuffled them to prevent information leakage through repeated access.

Figure 1: Memory Separation in Square Root ORAM
As shown in figure 1, the memory used for this scheme separates into three sections – the real blocks reserved for the actual data in the RAM, a shelter that acts like a "working memory", and dummy blocks (assume these are just set to 0) that help mask accesses when working with the shelter. At initialization, the shelter blocks are also assumed to be populated as dummy blocks.
Square Root ORAM works in "epochs" of \(\sqrt{N}\) memory accesses – over this duration, blocks are taken out of the real blocks and placed into the shelter. After an epoch, in the worst case, all of the blocks in the shelter will have been filled up by legitimate blocks with potentially updated data. The overall algorithm for a single epoch is as follows.
- Using the random function, map each logical and dummy block index onto a random tag via a random oracle \(\pi\). Tags are assumed to be on the range \([1, \frac{n^2}{\epsilon}]\), where \(\epsilon\) determines our collision probability.
- Make a single pass over all the permuted blocks to update their tag values. It is assumed that there is either an inverse mapping available from the previous epoch's tags, or the blocks are given encrypted metadata that identify their intended logical index.
- Implement Batcher's Sorting Network (a binary tournament sorting algorithm) to sort the permuted blocks by tag value.
- This network is used since its access pattern is identical irrespective of input data. We call such sorting algorithms an oblivious sort.
- Simulate \(\sqrt{N}\) memory accesses.
- Implement Batcher's Sorting Network over the entire memory, by the key \((v, \sigma)\). \(v\) is the index into the logical RAM (\(\infty\) for dummy blocks) and \(\sigma\) is 0 for permuted blocks, 1 for shelter blocks.
- Make a reverse scan through the ORAM, and mark each duplicate block as a dummy (e.g \(\sigma = 0\) for this block, but we saw \(\sigma=1\) the previous iteration).
The final sort is a bit ambiguous, but it works since we assume that the dummy blocks always have a tag \(\infty\). After step 5, these dummy blocks all end up in the final \(\sqrt{N}\) blocks – therefore any block with a valid tag must have been placed into the permuted blocks, effectively evicting the shelter. We also assume that the shelter will have at maximum one copy of each block (this will be clearer after explaining the access protocol), so after our sort we will find exactly one or two copies of each real block (hence \(\sigma\) allowing for a strict ordering).
Each access \((op_i, addr_i, data_i)\) of step 4 is performed as follows, where \(i \in [1, \sqrt{N}]\).
- Iterate over all \(\sqrt{N}\) blocks in the shelter.
- Read each block into the CPU.
- Update it to \(data_i\) if \(addr_i\) matches the block's metadata and \(op_i\) is a write.
- Re-encrypt the block and write back into the shelter.
- Select which block to read out of the permuted blocks.
- If the block was found in the shelter, we target \(tag_i = \pi(N + i)\) (the i-th dummy block).
- If we could not find it, we look for the real block by targeting \(tag_i = \pi(addr_i)\).
- Since we sorted the permuted blocks in step 3 of the epoch, we can perform an oblivious binary search to read out the block with \(tag_i\).
- The blocks are permuted every epoch, and each permuted block is accessed once per epoch.
- No information can be leaked about whether a dummy or real block was read, or reused.
- If the block was not found in the shelter and \(op_i\) is a write, update block data to \(data_i\). We then re-encrypt the block and write it into real block \(N + \sqrt{N} + i\) – e.g the i-th block of the shelter.
At a high level, we can outlined scheme fulfills some of the basic properties we desire from an ORAM. Both access types and block reuse cannot be leaked to an adversary, as every memory access uses an observably identical protocol. The reshuffling of permuted blocks further guarantees that we do not leak any information regarding data locality.
Furthermore, we can also see an improvement from our initial brute force scheme. The old scheme would have incurred a bandwidth of \(O(N\sqrt{N})\) per epoch. By incurring an additional client-side space overhead and a memory overhead of \(O(\sqrt{N})\), we reduce the per-epoch bandwidth to \(O(N\log^2N)\), which is dominated by the accesses required for Batcher's Search Network in steps 3 and 5 of each epoch.
Drawbacks
Despite being described as a "naive" solution by [2], this scheme presents some of the issues that plagued many ORAM schemes, the foremost one being complexity. It is difficult to intuitively reason about the correctness and operation of this scheme, and becomes even harder so when [2] later adapts it to a hierarchical solution.
There is also the non-trivial performance overhead - as explained earlier, this scheme requires significant storage overhead in the memory of an ORAM system, and the per-access latency (\(\approx \log^2N\)) does not scale well with memory sizes. Goldreich and Ostrovsky argue in section 6 of their paper that there must be a lower bound of \(\Omega(t\log{t})\) 1 real memory accesses to simulate \(t\) logical memory accesses on an ORAM.
Efficient Tree-Based ORAMs
Throughout the early 2000s, many ORAM schemes were devised to cut per-access bandwidth closer to this boundary. Efficient ORAM constructions like Pinkas-Reimann [5] and Goodrich-Mitzenmacher [6] still inherited from a hierarchical RAM scheme presented in section 5 of [2] and relied on oblivious sorting mechanisms. This meant that while amortized per-access ORAM latency approached logarithmic/polylogarithmic functions of N, worst-case latency was still on the order of \(\Omega(N)\) in [6] or \(\Omega(N\log N)\) in [5]. Altogether, this amounted in a performance overhead that ranged from 1400 to over 80000 times the number of operations required for the same access pattern with a transparent memory device [3] .
While some ORAM schemes around this time, like the SSS construction in [3] and Shi et al.'s \(\log^3\) ORAM [7], presented schemes that helped reduce the worst-case performance to polylogarithmic functions and reduce client/storage cost in doing so, tree-based constructions are currently the most popular category of ORAM. This is largely due to the innovations that came with the Path ORAM construction by Stefanov et al. [8].
Path ORAM
The general Path ORAM construction demonstrated in [8] inherits heavily from the previous work done by Shi et al. in [7], particularly in its usage of bucket-based storage trees with oblivious eviction.
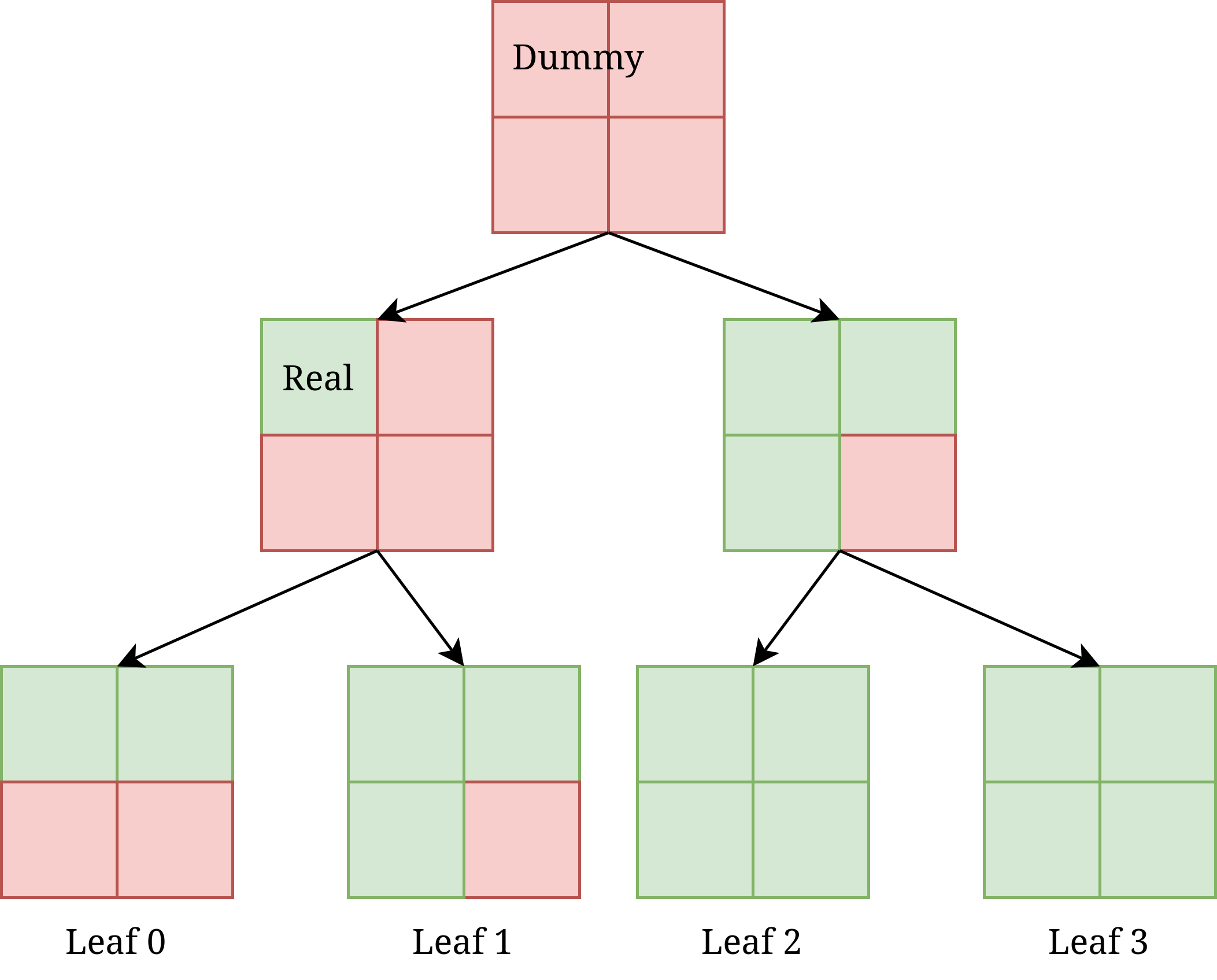
Figure 2: Path ORAM Memory Structure for \(Z=4, L=2\)
On the server side, storage is interpreted as an N-ary tree (typically binary) of \(L\) levels, where each node is a 'bucket' storing up to \(Z\) real memory blocks. Buckets with less than \(Z\) blocks will be padded with dummy blocks. An example of such a tree is laid out in figure 2. In the memory, these buckets would be laid out serially so they can still be accessed via a normal external indexing scheme.
Path ORAM, like most high-performance ORAM schemes, is also stateful on the client side. The client side must maintain a position map (\(\pi\)) to help it find a desired block inside the memory, as well as a stash (\(S\)) to store blocks in the client during runtime (more on this later). The position map is constructed such that indexing it with a block ID will return a leaf node in the memory's tree. The Path ORAM algorithm guarantees that when it traverses the tree to reach this leaf node, the desired block will be found in one of the buckets along this path (hence the algorithm's name).
It is assumed that at initialization, the client's stash is empty, the server only contains dummy blocks, and the position map is filled with uniformly random numbers corresponding to various leaf node indices. With this in mind, we outline the Path ORAM algorithm below for a single memory access \(\vec{y}_i\). We adopt the notation \(P(x)\) to denote the path from the root node to leaf node \(x\), and \(P(x, i)\) to denote the i-th node on this path.
- Load \(\pi(addr_i)\) into \(leaf_i\), then reassign \(\pi(addr_i)\) to a random leaf node.
- Load each of the buckets along \(P(leaf_i)\).
- Add the desired block \(addr_i\) to the stash \(S\).
- If \(op_i\) is a write, then update block \(addr_i\) to contain \(data_i\) in \(S\).
- Iterate backwards along the path that was traversed (leaf node upwards, e.g \(P(leaf_i, L)\) to \(P(leaf_i, 0)\)).
- At each bucket, select up to \(Z\) blocks from the stash that have this bucket somewhere on their path (per \(P(\pi(a))\) for some block \(a\)). Write them into the bucket.
- If we cannot find \(Z\) suitable blocks, write dummy blocks until the bucket is at capacity.
- Remove any blocks written to the bucket from our stash.
Like the Square Root ORAM [2] and our initial brute-force solution, every access using this algorithm looks identical for any observer. \(Z(L+1)\) blocks are read out of the memory and \(Z(L+1)\) blocks are written into it along some randomly selected path. Since the blocks are, in effect, evicted from the tree when read out and later relocated to a random location, we incur no risk of leaking data locality.
An interesting feature of this algorithm is the approach it takes to filling in the bucket tree at the end of each access. By taking a bottom-up traversion and pushing blocks as far down the tree as possible, buckets with fewer potential candidates are populated first. This in turn minimizes stash usage.
Performance and Usability Implications
As every access for Path ORAM is algorithmically identical, there is no need to calculate amortized latency. Since \(L\) is set to \(\log_2 N\) in a binary tree and \(Z\) is a fixed constant, the algorithm practically achieves logarithmic bandwidth \(O(\log N)\), even in the worst-case, for any practical block size. This surpassed the previous standard of \(O(\frac{\log^2 N}{\log(\log N)})\) for small-client-storage oblivious RAMs, a cuckoo hashing scheme set forth by Kushilevitz et al. in [9]. We only mention asymptotic results for now, as experimental results were only found for a construction in section Recursive Path ORAM.
On a related note, the failure probability of this algorithm is solely determined by potential path collisions when updating \(\pi\). If too many blocks are mapped to the same path, then a fixed-size stash \(S\) can potentially overflow. Accordingly, Stefanov et al. [8] constructed a novel proof structure characterizing the likelihood of stash overflow during the Path ORAM algorithm – this proof structure later became popular among other tree-based ORAM constructions. They were able to show that even at large security parameters (\(\lambda = 128\)) a stash of 147 blocks was sufficient for bucket size \(Z=4\). Notably, stash size is purely a function of \(Z, \lambda\), with no dependence on memory size \(N\). This made Path ORAM uniquely scalable to large memory sizes even with fixed client-side storage constraints. In practice, the paper experimentally found \(Z=4\) to be minimum required bucket parameter in order to prevent excessive stash accumulation, while stating that theoretically \(Z=5\) might be a better candidate.
There is also the benefit of usability – Path ORAM, despite being a hyper-efficient algorithm, is significantly easy to describe and construct when compared to older oblivious sorting and cuckoo hashing schemes (like the one in section Square Root ORAM). This made ORAM a much more feasible tool for not just cryptographers, but engineers and system architects to design secure systems.
Recursive Path ORAM
Despite the stash being invariant of memory size, the mapping table \(\pi\) inherently must be. For large \(N\), it becomes infeasible to store this on a client with limited storage.
Path ORAM borrows from ideas in [3] and [7], specifically with regards to moving mapping tables off-client via recursive ORAMs. To put it informally:
The 'big' ORAM's mapping table becomes an ORAM. Then that ORAM's mapping table becomes an ORAM. And then that ORAM's mapping table…
This procedure keeps going until a client requires suitably low amounts of storage to initiate an ORAM access. While this seems like it would pollute bandwidth, as indicated by a higher worst-case bandwidth \(O(\log^2 N)\), in practice Recursive Path ORAM still achieves R/W bandwidth of \(O(\log N)\). For a given access sequence \(\vec{y}\), this was experimentally determined by [4] to be approximately 160x the bandwidth of simply using an insecure memory. While this isn't directly comparable to the results on older schemes collected by [3], which were done using 64KB block sizes, there is a massive order of magnitude difference compared to older ORAM schemes. While this is less performant than the SSS construction in the same work, the relative simplicity and better client memory efficiency of Path ORAM made it significantly easier to iterate upon and implement in hardware-centric applications.
Ring ORAM
Ring ORAM, like Recursive Path ORAM, isn't so much a new algorithm altogether so much as it is a set of improvements to Path ORAM proposed by Ren et al. [4].
Ring ORAM's first goal was to reduce the amount of online bandwidth, which we can understand to be the required (non-amortized) bandwidth per access. To do so, they store additional encrypted metadata with each bucket containing a permutation – e.g which block is stored in each position of the bucket. This means that instead of loading every bucket along the path \(P(leaf_i)\), two accesses are made per bucket - one to query the metadata, and one to load the appropriate block afterwards.
A corollary of this approach is that we can no longer have an in-place eviction, as we'd be evicting many blocks out of each bucket prematurely (counter to the goal of reducing per-access bandwidth). Like the construction in section Square Root ORAM, Ring ORAM opts to periodically evict blocks in its lookaside storage (in this case, the stash instead of the shelter) back into the primary storage (buckets) and reshuffle when doing so.
Between the initial access and the reshuffle, the block is invalidated in the memory. To ensure we still read some block on every path traversion, a dummy block is read out in any case that the requested block address is not found in a bucket. To facilitate the dummy-pulling while employing a periodic eviction strategy, Ring ORAM makes a couple of modifications to Path ORAM's data model.
- Ring ORAM will store \(Z\) real blocks and \(S\) dummy blocks per bucket after each reshuffle. We retain the standard definition of a dummy block.
- An eviction is carried out either every \(A\) accesses (a tunable parameter) or when a single bucket is accessed \(S\) times without eviction (this is tracked via a counter). This latter condition is in place so that an argument regarding a block having to be real cannot be made per the pigeonhole principle prior to a bucket eviction.
With the above changes in place, we can make an additional optimization via an XOR. Since the requested block can only be found once on the traversion path, we can guarantee that we will either pull out \(L+1\) dummy blocks or \(L\) dummies and the requested block. Since dummies are assumed to always have a plaintext known to the client, we can assume that provided the nonces associated with each dummy, the client can generate the expected ciphertext for each dummy.
By returning an XOR of all the pulled data blocks from the memory, and then performing an XOR on the client side between this block and each of the locally generated dummy ciphertexts, we can still pull out the expected ciphertext of the real block. In doing so, the memory will only have to send back one effective data block on each path traversal, regardless of tree depth. In short, the per-access bandwidth becomes negligibly conditional on bucket size and tree depth. This is perhaps the biggest contribution of Ring ORAM – an online access bandwidth that is approximately identical to the expected bandwidth with insecure memory access.
As a whole, the improvements proposed by Ring ORAM reduce the bandwidth required for a single access without eviction from the tree to constant overhead. However since evictions are still required, the asymptotic amortized bandwidth (e.g average bandwidth over many accesses) is still \(O(\log (\frac{N}{A}))\), a logarithmic bound.
That said, this still translates to a practical performance improvement. Testing results in [4] showed that under the same 4KB testing scheme referred to in section Performance and Usability Implications, Ring ORAM with the XOR trick were able to bring overall bandwidth to only 60x the bandwidth required for insecure memory accesses. This is a little over \(\frac{1}{3}\) the bandwidth required for a recursive Path ORAM in the same scenario.
Related Research
In this section we, at a high level, discuss a variety of adjacent research endeavors that can leverage ORAM mechanisms as a facet of their system architecture or attempt to iterate on the construction of modern ORAM schemes.
Applications
While most of this primer discusses ORAM in a single-party context, the reality is that remote computation is rarely a single-client system anymore. In scenarios where a group of trusted users require concurrent and secure access to some remote memory, many single-client ORAM schemes can encounter coherency issues. As a minimum motivating example, we can look at the basic Path ORAM construction - there are possible scenarios where if you have 2 clients with stashes that contain real blocks, client A may unable to access a block that is temporarily held in client B's stash.
Anticipating this coherency problem, Goodrich et al. proposed a stateless ORAM mechanism for secure group data access [10]. Importantly, this mechanism requires that any client state be downloaded and re-uploaded to the remote when a client performs a memory access. As a result, any state maintained by the ORAM protocol should be lean to prevent bandwidth pollution. While constructions like SSS [3] may not be well-suited to this landscape due to high client storage requirements, a construction like Recursive Path ORAM [8] is better suited to this task. Its position map and stash can be maintained with only \(O(\log N)\) client storage and \(O(\log^2 N)\) bandwidth.
Another field with direct applications for ORAM is in secure processors. While there is a plethora of ongoing research regarding encrypted compute in enclaves and secure processors, we focus more on the utility of ORAM to mask program locality and memory access behavior. These architectures, approach memory interactions with a similar lens to the original Goldreich-Ostrovsky ORAM constructions [2], trying to mask information about the underlying program instructions that a secure processor is fetching out of RAM.
Simpler, more bandwidth-efficient constructions like Path ORAM that eschew in-memory sorts and shuffles lend themselves to better hardware representations. Hardware design generally benefits from eschewing large fully-associative structures and maintaining small fixed-bound iterations for anything repetitive. Both of these criteria are fulfilled by the Path ORAM model [8]. This is best embodied by some of the work done by Fletcher et al. in [11], [12].
Theoretic
We mentioned in section Drawbacks that [2] proved a lower bound on bandwidth of the form \(\Omega(t \log t)\) for \(t\) accesses. Notably, this bound is invariant of client memory size or block size.
However, this bound assumed an ORAM scheme based on oblivious sorting. Later papers like [13] showed that if a construction eschews this mechanism (like Path/Ring ORAM), a system can bring this bandwidth bound down to \(\Omega(t\log(\frac{tr}{c}))\) for \(t\) accesses, where \(r\) is the size of each block in an N-block memory and \(c\) is the size of client memory. This conclusion is much more in line with the optimizations that schemes like SSS in [3] make for large client memory sizes, and presents a harder target for novel ORAM schemes to pursue.
At the same time, many newer ORAM constructions were published after the Path and Ring ORAM papers that continued to optimize bandwidth under low client-side storage constraints, or relaxed other assumptions underpinning amortization of these schemes. A good example is OptORAMa [14], which achieved \(O(\log N)\) access bandwidth overhead for small memory word sizes and limited client-side memory. This improves upon the \(O(\log^2 N)\) overhead of prior constructions like Path ORAM in similar regimes. This improvement stemmed from Intersperse-based shuffling and more efficient hashing schemes (BigHT, SmallHT) used during reshuffling.
While modern constructions discussed in this primer are efficient enough to be used in real-world systems, future research will need to approach ORAM not just as a generic algorithmic tool but as something specialized to specific use cases. For example, future ORAM schemes with minimized eviction and shuffling and small stash sizes are likely to be more suitable for hardware implementation – a frontier that sees more relevance than ever in today's compute landscape.
References
Footnotes:
This assumes that the input program is large enough that \(\log t > 1\).